

栏目分类
发布日期:2024-08-20 02:35 点击次数:124

注:此为作家投稿【HND-037】現役キャンギャル中出し解禁!! ASUKA。投稿时期:2009年6月27日 16:18
对于舆图“四色问题”,本东谈主已写过三篇著作,其中于2007年5月21日发布在《少年百科》网站上的那篇《用减少法讲解最大平面图“四色问题”》 照旧用相配便捷的门径大概十足讲解最大平面舆图(即球面平面舆图)用四种面目填塞。对于这么纵情的问题,著作底下的驳倒中,除了少数东谈主默示看懂,大宗东谈主如故看不解白。在其它网站上登的不是莫得图,即是莫得看得懂的东谈主。 咫尺我再把原著作从头整理一下,增多了多幅评释的图,肯定唯有有初中(致使小学)数学常识的东谈主皆能看懂。 说明欧拉创立的“拓扑学”旨趣,平面舆图上无论花式何等复杂、大小何等不等的每块区域皆可行动一个点。而相互间有交界的可用连线来默示(从图1到图6每幅图上方的区域图皆可用底下的关连图来默示)。舆图上着色时唯有相互有交界的区域用的面目不同就能分清不同区域了,也即是关连图上每条线两头的点不重色就行了。 从最大平面图上看,每一个区域(点)皆是被其它些许个区域(点)所包围。底下咱们就逐个就各式包围情况来分析需要几种面目。 一个区域十足包围另一个区域的情况:这种情况肯定毋庸绘制大师也能明了,比如梵蒂冈处在罗马的包围之中,舆图上它唯灵验与罗马不同的任何面目就能诀别出来,而处在中间的梵蒂冈存在与否,压根不会影响罗马与周围区域的着色。
二个区域包围一个区域的情况:如图1所示,中间的区域唯灵验不同于外面二区域的任何面目就不错了,而它的存在与否,也压根不会影响外围二区域与其它区域的着色。即是说:在整个最大平面图中可把图1中左边的情况行动与右边的一样,下方的关连图即是去掉了中心O点,把二边形傍边两条边AB合并为一条。 三个区域包围一个区域的情况:如图2所示,中间的区域唯灵验不同于外面三区域的任何第四种面目就不错了,而它的存在与否,也压根不会影响外围三区域与其它区域的着色。即是说:在整个最大平面图中可把图2中左边的情况行动与右边的一样,下方的关连图即是去掉中心O点【HND-037】現役キャンギャル中出し解禁!! ASUKA,只剩下外面三边形ABC。 四个区域包围一个区域的情况:如图3所示,由于上与下区域不交界可用统一种面目、左与右区域也不交界也可用统一种面目,是以中间区域唯灵验第三种面目就行了。由于中间区域只与周围四个区域有交界,不与外界其它区域有交界,亚洲成人社是以它的存在与否,唯有外围四区域着色不变也不会影响其它区域的着色。即是说:在整个最大平面图中可把图3中左边的情况行动与右边的一样(图中是中间用了绿色使傍边区域连接,也不错用红色使高下区域连接),下方的关连图即是去掉中心O点,把C点合并到B点,只剩下三个点二条线。 五个区域包围一个区域的情况:如图4所示,周围五个区域中,A与C可用统一种面目,B与E可用另一种面目,D就必须用第三种面目,而中心的O就需要用第四种面目。由于中间区域与以上几种情况一样只与包围它的五个区域有交界,它的存在与否,唯有外围五区域着色不变也不会影响其它区域的着色。即是说:在整个最大平面图中可把图4中左边的情况行动与右边一样,下方的关连图即是去掉中心O点,把E点合并到B点,只剩下四个点四条线。 当外围的点增多时能否与上叙一样处理呢?禀报是详情的。咱们先来看一条公路状的平面图的着色(如图5、6所示),公路开始用一整块红色,傍边车谈向下对称的诀别用绿、红、绿、红……一块块涂色。当开始格外及傍边双方总块数加起来是偶数2n时,格外亦然一整块而且n是偶数也用红色,n是奇数用绿色(图5)。当开始格外及傍边双方总块数加起来是奇数2n-1时,格外傍边分两块,其中一块沿用上头车谈着色门径用红或绿,另一块就要多用一种面目蓝(图6)。中间用黄色把傍边车谈分离隔来,这么图5就需要三种面目,图6就需要四种面目。因为中间的黄色是被包围在公路当中不与外界战役,它的存在与否不会影响公路与外面地域的着色情况,是以不错把黄色部分去掉,去掉中间部分后傍边车谈就合二为一(如图中右边所示),图5和图6中右边与外界的着色关连同左边时仍旧一样。下方的关连图即是去掉中心点,通过合并,2n边形只剩下n+1个点n条线(图5),2n-1边形只剩下n+1个点n+1条线(图6)。带下划线的这两个规矩其实也符合上头所述的二边形、三边形、四边形、五边形……。它们仅仅多边形的几个特例。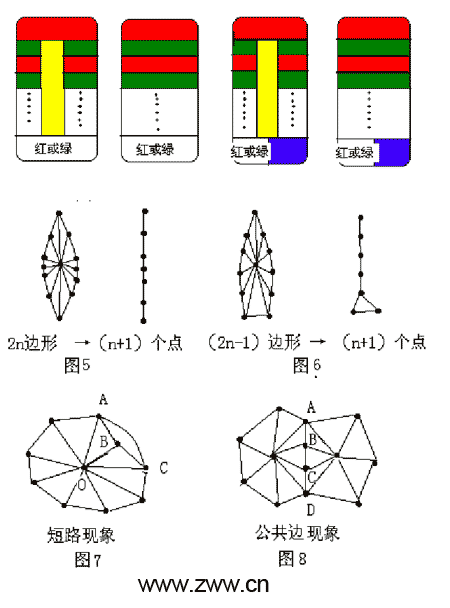
在最大平面图上不错把任何一个点当作中间点来回掉,但可能在包围这个点的多边形的各个极点当中有的点之间有连线(比如第1个点与第3、5、7等点有连线,相配于在串联电路中把一些电阻短路),这些点就不成使用统一种面目。图7中A与C的连线就把B点短路了,但一朝有短路风物就一定会产生比正本多边形边数少的多边形,如图7中就产生三边形AOC包围B点的情况,这么不错先去掉B点,正本的多边形也就少了一个B点。因为边数最少的多边形极点间不可能再有短路,是以唯有先找到整个最大平面图中极点最少的多边形进行去掉中心点(也即是贯穿线最少的点),再把外围的点按图1到图6的规矩进行合并。把减少合并后的线和点,在最大平面中代替正本多点包围极少的多边形(就象初等代数中解多元一次方程的代入消元法一样,用图1到图6的右面取代左面),再在新造成的整个平面图上找出极点最少的多边形,再用以上相通的门径把贯穿线最少的中间点去掉,把外围的多边形合并成几条线和几个点。这么一步步的减去、合并、代替下去,任何复杂的最大平面图到临了只剩下一个三边形。 在去掉中间点的进程中,很容易出现连成一串的四边形(如图8中的B和C皆是四边形的中心点),可先去掉B点把C与A合并,也可先去掉C点把D与B合并。从A点到D点执行上是两个多边形的大师边,在去掉这些四边形中心点的进程中,因为有着次第去掉一个合并一个的规矩,可一次性把这些点去掉,A到D的总点数是单数,合并后只剩下A点;A到D的总点数是双数,合并后只剩下A和D两点。 执行的舆图中通常有莫得中心点的多边形存在,也可用以上门径行动有中心点去掉后再把周围合并。在以上减去、合并、代入等操作进程中一直不会使用跳动四种面目。这就十足大概讲解任何复杂的最大平面图“四色填塞”。
[jyy630907@163.com]
用减少法讲解最大平面图“四色问题” [焦永溢 2007-5-21]
五月天情色透澈措置“四色问题” [焦永溢 2005-10-22]
对于“四色问题”的讲解 [焦永溢 2005-1-4] 【HND-037】現役キャンギャル中出し解禁!! ASUKA